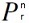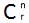STA 2023H Interesting Data
August 1st
We finished Chapter 8. We discussed Student t-distributions and what happens when you increase sample sizes. The critical value t* needs to be bigger for smaller sample sizes to make sure that the critical regions is still the same area.
We looked at a T-table:
T-table
We discussed how to use the calculator to find a t-interval: STAT, TESTS,8:, then input mean, standard deviation, sample size, and CI-level. The calculator outputs the interval.
We looked at some problems from Ex2S16.pdf which can be found in the discussion section of canvas. We did 1., 3. 4., 5., 6., 7., 8.
We then moved into the labs. I mentioned that you should look over problems involving when to use a 1-sample t-test versus 2-sample t-test. For matched pairs use 1-sample t-test on difference of scores.
We talked about correlation and the Pearson correlation coefficient R = rxy = r.
This is a measure of how linearly related two variables are: (X independent variable, Y dependent variable).
The closer |R| is to 1 the stronger the linear relationship.
R2 is called the variance and is the "proportion of the variance in the dependent variable that is predictable from the independent variable." We also say R2 is the percent of the variability between the variables that has been accounted for.
We showed how to construct a scatter plot on two columns.
=CORREL(X column, Y column)
Richt Click on a data point and then select Add Trendline. Then scroll down to click the box next "Display Equation on Chart" and "Display R-squared value on chart".
The least squares regression line is ŷ = b x̂ +a.
Here b = r sy/sx. The line goes through the point (x̄ ȳ).
Notice that b is positive if and only if r is negative. So negative correlation means inverse relationship.
This line is the unique that minimizes the sum of the squares of residuals.
=FORECAST.LINEAR(x, Y column, X column) will produce the output of plugging in x into the least squares regression line.
July 20th
We reviewed a bit more on probability. Showed that a full house has .00144 probability. I found this site that has all of the kinds written out.
Poker Hands
We discussed why the probability of rolling a double with 2 dice is 1/6; similar to rolling a sum of 7.
We collectively rolled the dice 258 times, with an expected value of 43 rolls of a sum of 7, and 43 doubles. We got 42 7s, and 41 doubles.
We concluded our discussion on normal distributions. We again discussed the z-score as well as percentiles.
We used the calculator to get from a data point to percentile; use normalcdf(lower, upper,μ, σ).
We discussed how to get from a percentile back to a data point as well as z-score: invnorm(p,μ, σ).
Took 3 quizzes. One had to do with a chart and how to read the conditional probability. One had to do with simple card probabilities. The third had to do with z-scores and percentiles.
We briefuly discussed problems with surveying and sampling. We came up with a question of how often do adults between the ages 40 and 60 exercise (in minutes). We decided maybe should restrict to S. Floridians.
We would sample and compute the sample mean x and sample st. dev. Sx. We do not say this is the mean for the population.
However, when things are done properly we can say that we are 95% confident that the real mean μ is in an interval around x.
We went into the computer lab for a brief amount of time and discussed the following excel functions:
=NORM.DIST(x,μ, σ, TRUE) This returns the percentile of a given data point with a mean μ and a st. dev σ.
=NORM.S.DIST(zx, TRUE) This returns the percentile of a given z-score.
=NORM.INV(p,μ, σ) This returns the score from a given percentile with a mean μ and a st. dev σ.
=NORM.S.INV(p) This returns the z-score from a given percentile.
=STANDARDIZE(x,μ, σ) This returns the z-score given the information.
Here is a link to a sample test.
Stat Trek
Problems 2., 6., 9., 14., 18., 26., 30., 31., 34., 38. are on topics that will be on Tuesday's test.
July 18th
We concluded our discussion on probabilities. We reviewed a bit on binompdf(n,p,k) and binomcdf(n,p,k), tree diagrams.
We showed using excel that a binomial distribution is a normal distribution.
The expected value (i.e. mean) of a binomial distribution is E(X)=np, while the standard deviation is σ= √[np(1-p)]
We started a discussion on normal distributions.
N(μ , σ) denotes a normal distribution with mean μ and standard deviation σ.
The standard normal distribution is N(0,1). Standardizing scores means converting to a standard normal distribution. This is done by finding a scores z-score.
z = (x- μ) / σ
A negative z-score represents a score that is below the mean, while a positive z-score represents a score above the mean.
The emperical rule 68%-95%-99.7% is that 68% of the data falls within 1 st. dev. away from the mean, 95% of the data falls within 2 st. dev. away from the mean, 99.7 of the data falls within 3 st. dev. away from the mean.
We use a z-table to convert a z-score to a percentile. Here is a link to the first one that pops up on google. z-table
Also use the calculator normalcdf(lower,upper, μ , σ)
July 13th
We discussed conditional probabilities. P(A|B) = |A ∩ B| / |B| = P(A ∩ B) / P(B).
We defined two events A and B to be independent if P(A|B)=P(A). We then showed that the events are independent if and only if P(A ∩ B) - P(A) P(B).
We discussed tree diagrams. This led to a discussion on binomail distributions. e.g. success/failure
Given n trials, X is the random variable of how many successes there are. P(X=r) = 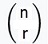 pr (1-p)n-r.
pr (1-p)n-r.
We showed how to use the calculators. Click 2nd Dist, then scroll to: binompdf(n,p,r) = P(X=r), while binomcdf(n,p,r) = P(r ≤ X).
We walked over to the tennis courts and discussed the game of tennis in anticipation of our data project. We discussed 1st serve, 2nd sreves, double faults, let serves, aces, etc.
We use a tree diagram to calculate the percentage of points won by a server.
We used a tree diagram to show that the probability of winning craps is 49.2%
Next, class I will go over 4.3 and Chapter 5.
July 11th
In the first half of the class we had a more theoretical discussion of probability.
1) outcomes, sample space, and events (simple and compound)
2) P(A) = |A|/|S|
3) Properties of P( )
a) 0\leq P(A) \leq 1: P(empty set)=0, P(S)=1
b) P(not A) = 1 - P(A)
4) We discussed Venn diagrams and complement, union, and intersection.
5) P(A or B) = P(A) + P(B) - P(A and B)
6) Two events, A and B are mutually exclusive if A and B is empty.
7) The number of permutations of n objects is n! (n factorial). (A permutation is an ordered arrangement of the objects.)
8) We discussed nPr and nCR and how to get on TI83/84
nPr = n! / (n-r)! = 
nCr = nPr / r! = n!/ [r! (n-r)!)] = 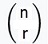 =
= 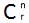
Turns out that the latest version of Excel allows you to create a modified box-whisker plot.
July 6th
Today we discussed the formal definition of an outlier. The data xi is an outlier if either
xi ≥ Q3 + 1.5 x IQR or xi ≤ Q1 - 1.5 x IQR
We discussed the box-and-whiske plots and how to gain information from them.
We talked about stem and leaf plots as well as comulutative frequency distributions.
Then we began a discussion on probability. We defined the sample space, an event, the probability of an event. We looked at many examples: flipping a coin, rolling a die (different sided die), drawing 2 cards at random without replacement, rolling two die and taking their sums.
For drawing n cards, a hand is a set of n many cards, order does not matter. The number of 5 card hands is 2,598,960. A pair is a set of two cards with the same number/letter. We defined a 5 card hand to be a pair if it has exactly one pair. We computed the probability of drawing a pair to be p=.4226. We discussed the game of craps and left it as a HW problem to calculate the probability of winning. You can google how to play craps. The basic idea is
1) if you roll a 7 or 11 then you win,
2) if you roll a 2,3, or 12, then you lose,
3) any other role is called the point. To win you must roll the point before you roll a 7 (keep rolling til you either roll the point or roll a 7). if you roll a 7 first you lose.
What is the probability of winning the game?
June 29th
Hi there,
To recap we covered Chapters 1 and 2 today in class. I mentioned that you should read about frequency distributions and specifically cumulative. I also mentioned that next Thursday is Test 1 but this is incorrect as many of you pointed out. My apologies for the wrong message. Test #1 is on Tuesday the 11th. This was an oversight on my part.
We discussed the following main topics:
center, spread, mode discrete v. continuous, range, 5 number summary, IQR. deviation, standard deviation (sample versus population), box-and-whisker plots, distributions including symmetric versus skewed left, skewed right, unimodal, bimodal, percentiles, quartiles
We also discussed how to input data into a list on the TI-84 as well as compute 1-var statistics. We showed how to create charts in excel (e.g bar graphs, pie charts, histograms) and we manipulated them a little bit (e.g bar graphs, pie charts, histograms and their bins). We discussed when to use which one depending on whether quantitative or categorical data.
On next Thursday we will go over some other distributions as well as outliers. Please plan on bringing in a deck of cards and a pair of dice. If you have a quarter or two to bring that would be great as well.
You should be able to do the problems in the review sections of both chapters. Pay special attention to outliers, cumulative frequency distributions, and stem-and-leaf plots.
June 27th
Hi there,
I published the course on canvas. Please have a look and let me know if you can get to it. You should be able to find a link to my webpage, the syllabus, and the list of HW problems.
You should start reading chapter 1 with an emphasis on sections 1.3 and 1.4. In 1.3 you can find information about mean and median as well as percentiles. There are directions there on how to input data into your calculator (TI-84) and how to compute some statistics on the data.
On Thursday I will talk about measures of spread as well as Chapter 2 and visualizations of data. We will go into the lab and start learning how to use excel.
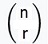 pr (1-p)n-r.
pr (1-p)n-r.